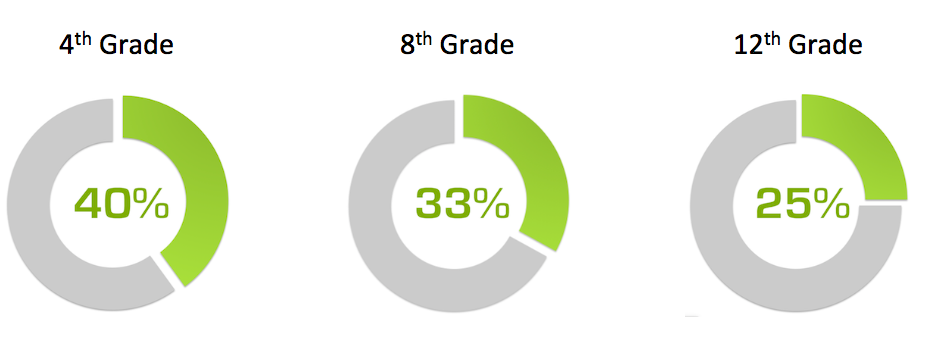
In 2015, only 40% of 4th graders, 33% of 8th graders, and 25% of 12 graders scored proficient or better in US standardized mathematic assessments.
Early childhood mathematics is vitally important for young children's present and future educational success. Research demonstrates that virtually all young children have the capability to learn and become competent in mathematics. Furthermore, young children enjoy their early informal experiences with mathematics.
 Children behind in third grade rarely catch up.
Children behind in third grade rarely catch up.
Unfortunately, many children's potential in mathematics is not fully realized, especially those children who are economically disadvantaged. This is due, in part, to a lack of opportunities to learn mathematics in early childhood settings or through everyday experiences in the home and in their communities. Improvements in early childhood mathematics education can provide young children with the foundation for school success.
Source: National Research Council; Division of Behavioral and Social Sciences and Education; Center for Education; Committee on Early Childhood Mathematics; Christopher T. Cross, Taniesha A. Woods, and Heidi Schweingruber, Editors

Current research shows that:
Too many school programs focus entirely on mastery of computation and memorization of facts. Unfortunately, kids who don’t have an understanding of mathematical concepts in the early years, rarely catch up – regardless of remedial strategies employed. MathBRIX addresses the problem by focusing on the understanding of concepts underlying the notation, rather than drill and practice.
Source: A joint position statement of the National Association for the Education of Young Children (NAEYC) and the National Council of Teachers of Mathematics (NTCM).
MathBRIX is built upon the premise that perplexing situations will catch students’ imagination or motivate them to learn whatever is necessary in order to solve the posed problem. As students work through repeated exposures to the content, they encounter interlocking experiences of increasing sophistication. The pedagogy is derived from the federally-funded Comprehensive School Mathematics Program (CSMP), a constructivist model of learning “by doing” produced and disseminated from 1970 to 2000. The program incorporated math stories, inventive "visual languages" and unique uses of math manipulatives. Fifty studies over a 20-year period found that CSMP students – in all subgroups – scored statistically better on problem-solving and concept understanding than all others. However, in a paper-based class with a preponderance of math manipulatives, it took an overwhelming amount of time for teachers to plan and differentiate instruction for every student in real time. MathBRIX's adaptive platform takes the burden off the teacher by handling individualization, manipulative tracking, data collection and record keeping in mixed ability classrooms.
Source: McREL, (1984) Comprehensive School Mathematics Program, (Final Evaluation Report)

CSMP was a forerunner to several of the popular conceptually-focused core programs, such as Singapore and Eureka Math. Like CSMP, they adhere to Jerome Bruner's three-step learning process: concrete > pictorial > abstract. In the concrete step, students engage in hands-on learning experiences using physical objects, commonly called math manipulatives. This is followed by drawing representations of mathematical concepts. Students then solve mathematical problems in an abstract way by using numbers and symbols. MathBRIX is an ideal companion to these in-school programs as they can extend time on task in a fun and challenging way.
Source: Bruner, Jerome, (1961) The Process of Education, p. 33.
Experts agree that manipulatives play a helpful role in the teaching of concepts, especially for children struggling with math. However, too many schools forego the benefits of concrete manipulation as it is difficult to manage and assess student performance for an entire class. Dr. Jo Boaler, Professor of Mathematics Education at Stanford University and author of Mathematical Mindsets, strongly advocates teaching children mathematical concepts from a very early age. She recommends teaching with technology and manipulatives, as they invite students into visual and conceptual thinking.

Source: Boaler, Jo, (2016) Mathematical Mindsets, Publishers Jossey-Bass, San Francisco
MathBRIX adheres to the principles of Universal Design for Learning and present information in visual, audio and hands-on ways. It offers more than one way for students to access the same material and use different methods to show what they know. A multi-sensory approach is particularly helpful for young children as well as those with learning and attention issues.
Studies show that a multisensory approach and hands on math tools - the foundation of MathBRIX - boost mental math skills and address these learning problems head-on.

Universal Design for Learning principles are followed in the development process to better accommodate learning disabled and special needs students. Special product features include: (1) multiple means of representation; (2) visual schedule based on previous activities; (3) text to speech, spoken word when icons are touched; (3) dynamic skill levels; (4) attention to color keys/contrast, button/font size; (5) student-friendly level advancement; no negative feedback; (5) awards recognizing and celebrating progress: time on task, finishing a task, memory exercises and of course, math accomplishments; (6) user feedback.
Source: CAST, About Universal Design for Learning

MathBRIX is designed with a spiral or “spaced” approach – a research-based recommendation in the 2007 IES Practice Guide. Concepts are revisited repeatedly, gradually increasing in complexity. Problem-solving strategies incorporated are also outlined in the 2012 IES Practice Guide: (1) posing problems, (2) thinking about problems, (3) visual representations, (4) multiple problem-solving strategies, and (5) recognizing and articulating concepts. Follow-on activities are performance-based – rather than by grade level – with results tracked.
Sources: (1) US Department of Education, IES Practice Guide, 2007. Organizing Instruction and Study to Improve Student Learning US; (2) Department of Education, IES Practice Guide, 2012. Improving Mathematical Problem Solving in Grades 4 Through 8